Площадь сегмента сферы: формула расчета и примеры решения задач

Геометрические фигуры широко используются в науке и технике для моделирования реальных объектов. Одной из таких фигур является сегмент сферы – часть сферической поверхности, отсеченная плоскостью. Знание формулы для вычисления площади сегмента сферы позволяет инженерам и архитекторам оптимально рассчитывать различные конструкции, а художникам и дизайнерам – создавать реалистичные модели.

Что представляет собой сегмент сферы

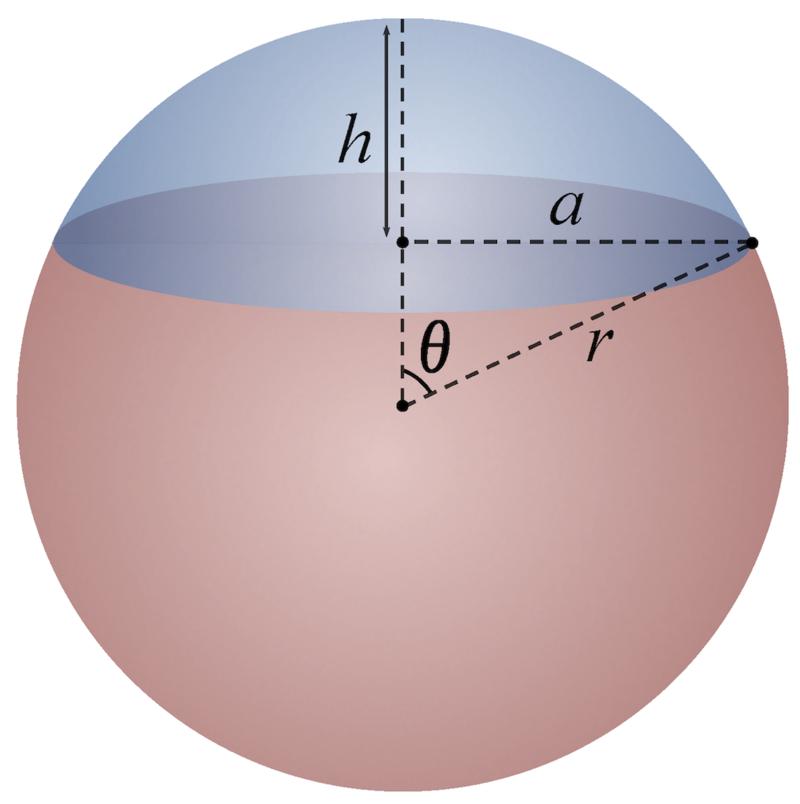
Сегмент сферы получается, если пассечь сферу плоскостью. На рисунке ниже сегмент сферы выделен синим цветом:

Как видно из рисунка, сегмент сферы состоит из двух частей:

• Плоского основания, которое представляет собой круг
• Выпуклой боковой поверхности

Для однозначного задания сегмента сферы необходимо знать радиус сферы R, радиус основания сегмента r и его высоту h. Между этими величинами существует связь.

Зная любые две из этих величин, третью можно найти по приведенной формуле.

Формула для расчета площади сегмента сферы

Площадь сегмента сферы равна сумме площадей составляющих его частей – плоского основания и выпуклой боковой поверхности:

• Площадь основания Сосн рассчитывается по формуле площади круга.
• Площадь боковой поверхности Сбок является частью площади сферы (сферический пояс) и рассчитывается по формуле.

Сложив эти площади, получаем общую формулу.

Рассмотрим пример использования этой формулы. Дан шар радиусом 6 см. Найдем площадь сегмента сферы, если известно, что его высота равняется 2,4 см, а радиус основания – 4,7 см. Подставляем значения в формулу и решаем задачу.

Таким образом, полная площадь сегмента сферы в данном случае составляет 83,63 см2.

Формула позволяет находить площадь при разных значениях радиуса сферы R, высоты сегмента h и радиуса его основания r. Зная только два из этих параметров, третий можно рассчитать по приведенной в начале формуле связи радиусов.

Применение формулы для решения практических задач

Рассмотренная формула для вычисления площади сегмента сферы широко используется в самых разных областях:

• При проектировании куполов, крыш, резервуаров и других архитектурных конструкций
• В скульптуре и дизайне для моделирования поверхностей
• В технике для расчета площади покрытий и облицовок
• Для решения геометрических оптимизационных задач на нахождение наименьшей или наибольшей площади

Расчет площади покрытия резервуара

Например, требуется определить, какое количество краски потребуется для окраски внутренней поверхности сферического резервуара радиусом 5 м, если краска расходуется с интенсивностью 0,2 кг на 1 м2. Решение:

1. Находим радиус внутренней поверхности резервуара: R = 5 м
2. Задаем высоту сегмента равной радиусу сферы: h = R = 5 м
3. Тогда радиус основания сегмента тоже будет равен радиусу сферы: r = R = 5 м
4. Подставляем значения в формулу и находим площадь сегмента сферы
5. Умножаем найденную площадь на расход краски в 0,2 кг/м2. Получаем, что нужно 300 кг краски.

Задача на нахождение оптимальных размеров

Инженер-конструктор проектирует укрытие из шаровых сегментов для защиты оборудования от осадков. Определите оптимальный радиус сферы R и высоту сегмента h, при которых площадь сегмента сферы будет минимальной, если известно, что радиус основания сегмента должен быть равен 1,5 м.

Решение:

1. Задаем радиус основания: r = 1,5 м
2. Ищем экстремум функции S(R,h) при заданном значении r
3. Приравниваем производную по h к нулю и находим оптимальное значение h:
4. Подставляем найденное значение h в формулу связи радиусов и находим R = 3 м
5. Подставляем оптимальные значения R и h в формулу площади. Получаем минимальную площадь сегмента сферы, равную 13,3 м2.

Таким образом, оптимальный радиус сферы равен 3 м, а высота сегмента – 1,5 м.

Рекомендации по применению формулы

Чтобы правильно рассчитать площадь сегмента сферы, следует:

• Выбрать подходящую формулу в зависимости от известных исходных данных
• Аккуратно подставить численные значения в формулу
• Проверить правильность вычислений
• При необходимости упростить или преобразовать конечное выражение

Основные типы ошибок:

1. Неверный выбор формулы
2. Неправильная подстановка значений
3. Неправильное упрощение выражений
4. Неверный ответ из-за ошибок округления промежуточных значений

Чтобы их избежать, рекомендуется проводить оценку правдоподобия полученного ответа.

Перспективы дальнейшего исследования

Тема вычисления площадей сегментов сферы тесно связана с другими областями математики и имеет большой потенциал для дальнейшего изучения. В частности, представляет интерес:

• Обобщение формул на сегменты эллипсоидов и параболоидов
• Разработка численных методов вычисления в сложных случаях
• Создание компьютерных программ и приложений для автоматизации расчетов

Кроме того, многие вопросы до сих пор остаются открытыми, например, задачи оптимального разбиения фигур на сегменты сферы заданной площади. Такие задачи представляют не только теоретический, но и большой практический интерес.