Отрицательные числа — целые значения меньше нуля

Отрицательные числа — это целые числа меньше нуля. В отличие от положительных чисел, они обозначаются со знаком «минус» и используются для представления величин противоположных положительным, например температуры ниже нуля градусов по Цельсию. Отрицательные числа широко применяются в математике, физике, экономике и других областях.

В этой статье мы разберем, что такое отрицательные числа, где они используются, и как выполнять арифметические действия с отрицательными числами.

Определение и применение

Отрицательные целые числа — это числа, расположенные слева от нуля на числовой прямой. Они меньше нуля и обозначаются знаком «минус» перед числом. Например: -5, -12, -1024. Целые положительные числа расположены справа от нуля и больше нуля. Например: 1, 5, 10, 12345.

Отрицательные числа широко используются для обозначения величин, противоположных положительным. Например, температура ниже нуля градусов, долги, потери и убытки в бизнесе. Они позволяют описывать процессы уменьшения и понижения различных величин.

Без отрицательных чисел невозможно было бы описать многие реальные процессы и явления. Например, баланс банковского счета, температуру воздуха зимой, глубину залегания полезных ископаемых. Отрицательные числа дополняют набор математических инструментов и расширяют возможности математических расчетов.

Действия с отрицательными числами

Целые отрицательные числа можно складывать, вычитать, умножать и делить так же, как и целые положительные числа. При этом действуют те же правила и закономерности. Рассмотрим основные действия с отрицательными числами.

• Сложение отрицательных чисел выполняется по обычным правилам сложения. Например: (-5) + (-3) = -8.
• Вычитание отрицательных чисел также не отличается от стандартного вычитания. Например: (-10) — (-6) = -4.
• При умножении двух отрицательных чисел получается положительное число. Например: (-2) • (-3) = 6.

Особое внимание стоит уделить сложению и вычитанию положительных и отрицательных чисел:

Таким образом, действия с отрицательными числами целиком подчиняются математическим законам и логике. Главное — понимать их смысл и последовательно применять правила при вычислениях.

Свойства отрицательных чисел

Отрицательные числа обладают определенными свойствами, которые позволяют выполнять с ними различные математические операции. Рассмотрим основные свойства целых отрицательных чисел.

1. Свойство противоположных чисел. У любого числа есть противоположное число, которое отличается от него знаком. Например, противоположным для 5 является -5.
2. Свойство нулевого элемента. При сложении любого числа с его противоположным результат равен нулю. Например, 5 + (-5) = 0.
3. Свойство обратного порядка следования. Целые отрицательные числа располагаются на числовой оси в обратном порядке — от -1 до бесконечности.
4. Свойство аддитивной инвариантности. Порядок сложения не влияет на результат. Например, (-3) + (-5) = (-5) + (-3).
5. Свойство аддитивной идемпотентности. Любое число, сложенное с самим собой, даст это же число. Например, (-7) + (-7) = -14.
6. Свойство коммутативности умножения. Порядок множителей не влияет на результат. Например, (-2) • (-5) = (-5) • (-2).
7. Свойство ассоциативности сложения. Сумма не зависит от скобок в выражении. Например, (-1) + ((-3) + (-2)) = ((-1) + (-3)) + (-2).

Благодаря этим и некоторым другим свойствам со всеми целыми отрицательными числами можно производить арифметические действия по стандартным правилам. Понимание свойств позволяет избежать ошибок при работе с отрицательными числами.

Особенно важно запомнить:

• Сложение с противоположным числом дает ноль.
• Вычитание противоположного числа эквивалентно сложению с ним.
• Умножение двух отрицательных чисел дает положительный результат.

Понимание свойств отрицательных чисел позволяет не только выполнять вычисления, но и решать текстовые задачи, в которых используются отрицательные величины. Это очень расширяет область применения целых отрицательных чисел в реальной жизни.

Графическое изображение отрицательных чисел

Для наглядного представления целых отрицательных чисел используется числовая прямая или ось. Она позволяет изобразить соотношение и расположение всех целых чисел отрицательных, положительных и нуля.

Числовая ось строится следующим образом:

• В центре проводится вертикальная линия, обозначающая ноль.
• Справа от нуля располагаются положительные числа в возрастающем порядке.
• Слева от нуля располагаются отрицательные числа в убывающем порядке.

Таким образом, точка на оси однозначно определяет какое-либо целое число. Например, точка, расположенная левее нуля на расстоянии 3 единиц, соответствует числу -3. А точка, расположенная правее нуля на расстоянии 5 единиц, — числу 5.

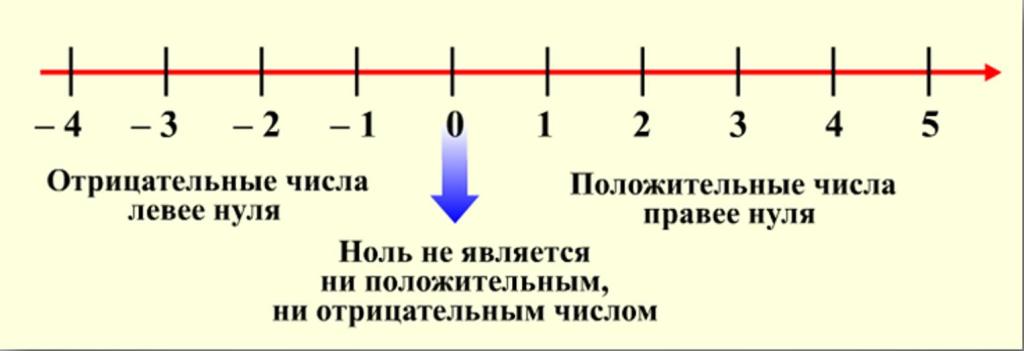
С помощью числовой оси наглядно изображаются:

• Сравнение целых чисел. Больше то число, точка которого расположена правее на оси.
• Сложение и вычитание. Складываемые числа откладываются в одну сторону от нуля, а результат — в эту же сторону.
• Умножение и деление. Результат умножения положительного и отрицательного чисел откладывается в положительную сторону, деления — в отрицательную.

Также для наглядности используются графики функций, где по оси X откладываются значения аргумента, а по оси Y — значения функции. Это позволяет визуализировать зависимости, содержащие отрицательные величины.

Изображение целых отрицательных чисел на числовой оси или координатной плоскости существенно облегчает понимание их свойств и взаимосвязей. Графические методы широко используются как в теоретической математике, так и в прикладных задачах.

Применение отрицательных чисел

Целые отрицательные числа находят весьма широкое применение в различных областях науки, техники и повседневной жизни. Рассмотрим основные примеры использования отрицательных чисел.

В физике отрицательные числа позволяют описывать векторные величины, такие как скорость, ускорение, сила, импульс. Например, скорость движения тела влево по оси X будет отрицательной.

В электротехнике отрицательные числа используются для обозначения направления электрического тока и напряжения. Потенциал заземления принимается за 0 В, а напряжение источника тока может быть как положительным, так и отрицательным.

В термодинамике отрицательные температуры используются при описании сверхнизких температур. Абсолютный нуль (-273,15 °С) принимается за начало термодинамической шкалы.

В географии и картографии отрицательные значения широты используются для обозначения координат точек южного полушария Земли.

В авиации отрицательные числа показывают высоту полета ниже уровня моря. Например, -100 метров означает высоту в 100 метров ниже уровня моря.

В финансовой математике отрицательные числа используются для обозначения долгов, убытков, расходов. Отрицательное сальдо на счете означает задолженность.

В программировании отсчет индексов элементов массивов часто начинается с отрицательного числа. Также отрицательные числа могут обозначать специальные значения, например ошибку.

В лингвистике отрицательные числа используются в векторных моделях для формализации семантических отношений между словами и понятиями.

В психологии по шкале Цунга отрицательные баллы соответствуют наличию депрессивных симптомов у человека.

В искусстве и дизайне отрицательное пространство играет важную роль в композиции произведения.

В быту отрицательные числа используются для обозначения низких температур, задолженностей, показателей времени до наступления события и других величин.

Как видно из примеров, отрицательные числа являются важным математическим инструментом, позволяющим описывать противоположно направленные векторные величины, обратные величины, а также дополняющие положительные числа симметричные значения различных показателей.