Плоскость и прямая в пространстве: решение задач

Вступление в статью с полезной информацией. Рассматривается взаимное расположение плоскости и прямой в трехмерном пространстве. Анализируются различные случаи: пересечение, параллельность, принадлежность. Приводятся конкретные примеры решения задач.

Даются рекомендации по составлению уравнений плоскостей и прямых в пространстве. Объясняются основные приемы решения типовых задач на данную тему.

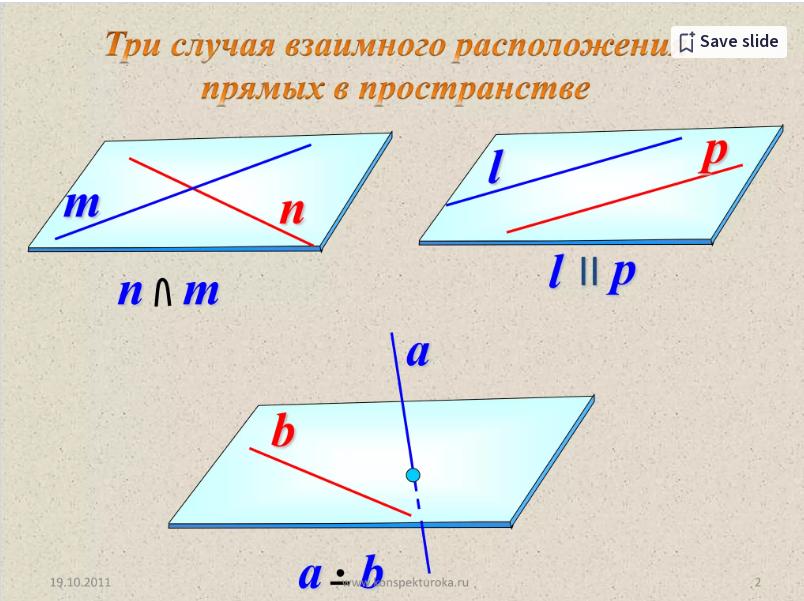
Случаи взаимного расположения плоскости и прямой в пространстве

Существует три основных варианта взаимного расположения плоскости и прямой в трехмерном пространстве:

1. Прямая пересекает плоскость в некоторой точке.
2. Прямая параллельна плоскости.
3. Прямая целиком лежит в плоскости.

Для определения характера взаимного расположения используют вектор нормали плоскости и направляющий вектор прямой. Если их скалярное произведение равно нулю, прямая параллельна или лежит в плоскости. В противном случае прямая пересекает плоскость.

Чтобы понять, параллельна прямая плоскости или лежит в ней, подставляют координаты произвольной точки прямой в уравнение плоскости. Если точка удовлетворяет уравнению, значит прямая лежит в плоскости, иначе — параллельна ей.

Пересечение плоскости и прямой в пространстве

Если прямая пересекает плоскость, то существует точка, которая принадлежит одновременно прямой и плоскости. Чтобы найти координаты этой точки, используют параметрические уравнения прямой и уравнение плоскости.

Подставляют параметрические координаты некоторой точки прямой в уравнение плоскости и получают уравнение относительно параметра t. Решив его, находят значение параметра, соответствующее точке пересечения. Подставляя это значение в параметрические уравнения прямой, получают координаты искомой точки.

Таким образом, для нахождения точки пересечения прямой и плоскости нужно решить систему уравнений: параметрические уравнения прямой и уравнение плоскости относительно параметра. Это основной способ нахождения точки их пересечения в пространстве.

Рассмотрим численный пример такой задачи.

Параллельность прямой и плоскости в пространстве

Прямая и плоскость в пространстве могут быть параллельны. Это означает, что они не пересекаются при любом своем взаимном расположении.

Чтобы определить, параллельны ли данная прямая и плоскость, используют их уравнения. Скалярное произведение вектора нормали плоскости и направляющего вектора прямой должно быть равно нулю.

Еще один способ — подставить координаты некоторой точки прямой в уравнение плоскости. Если точка не удовлетворяет уравнению, значит прямая параллельна плоскости.

Так определяют параллельность прямой и плоскости в пространстве, не выполняя построение.

Принадлежность прямой плоскости в пространстве

Еще один вариант взаимного расположения прямой и плоскости в пространстве — когда прямая целиком лежит в плоскости.

В этом случае любая точка прямой удовлетворяет уравнению плоскости. Чтобы определить, лежит ли прямая в плоскости, достаточно подставить координаты одной ее точки в уравнение плоскости.

Если подстановка координат точки прямой в уравнение плоскости приводит к верному равенству, значит, прямая лежит в данной плоскости.

Принадлежность прямой плоскости определяется подстановкой координат точки прямой в уравнение плоскости и проверкой выполнения равенства.

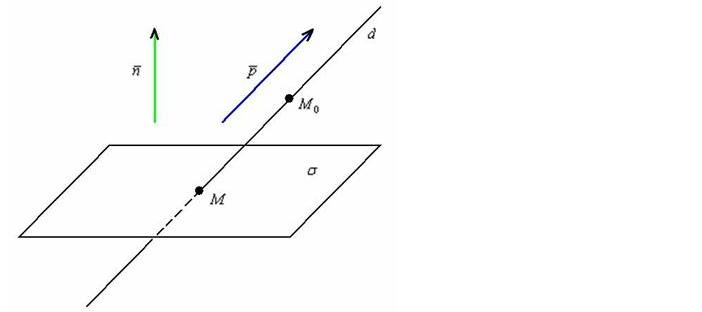
Нахождение точки пересечения плоскости и прямой

Если известно, что прямая пересекает плоскость в пространстве, важной задачей является нахождение координат точки их пересечения.

Для этого используют параметрические уравнения прямой и общее уравнение плоскости. Подставляют координаты точки прямой в уравнение плоскости и получают уравнение относительно параметра.

Решая это уравнение, находят значение параметра, соответствующее точке пересечения. Подставляя найденное значение обратно в уравнения прямой, получают искомые координаты точки.

Построение плоскости, перпендикулярной данной плоскости или прямой

В пространственной геометрии часто нужно построить плоскость, перпендикулярную некоторой заданной плоскости или прямой.

Чтобы построить плоскость, перпендикулярную данной плоскости, используют вектор нормали этой плоскости. Он же будет вектором нормали искомой перпендикулярной плоскости.

Для построения плоскости, перпендикулярной заданной прямой, берут направляющий вектор этой прямой. Он задает направление нормали к искомой плоскости.

Зная вектор нормали, строят уравнение перпендикулярной плоскости через заданную точку или прямую. Таким образом находят плоскость, перпендикулярную объекту в пространстве.

Нахождение проекции точки или прямой на плоскость

Проекцией точки или прямой в пространстве на плоскость называется их ортогональное проецирование на эту плоскость.

Для нахождения проекции точки проводят из нее перпендикуляр к плоскости и находят его точку пересечения с плоскостью — она и будет проекцией.

Чтобы найти проекцию прямой, используют метод пересечения плоскостей. Строят вспомогательную плоскость, проходящую через прямую и перпендикулярную заданной плоскости. Проекцией прямой будет линия их пересечения.

Так находят ортогональные проекции точек и прямых на плоскость в пространстве.

Вычисление угла между объектами

Для вычисления угла между плоскостью и прямой в пространстве используется формула, основанная на скалярном произведении вектора нормали плоскости и направляющего вектора прямой. Если прямая перпендикулярна плоскости, то угол между ними равен 90 градусов.

• Вектор нормали плоскости берется из ее уравнения в виде Ax + By + Cz + D = 0.
• Направляющий вектор прямой берется из параметрических уравнений прямой.

Формула для вычисления угла θ между плоскостью и прямой в пространстве имеет вид: cosθ = |(N, V)| / (|N| * |V|), где N — вектор нормали плоскости, V — направляющий вектор прямой. Под корнем берется модуль скалярного произведения векторов, чтобы убрать возможный минус.

Элемент уравнения	Обозначение
Вектор нормали плоскости	N
Направляющий вектор прямой	V

Зная уравнения плоскости и прямой в пространстве, можно вычислить угол между ними по приведенной выше формуле.

Примеры решения задач

Рассмотрим несколько примеров с решением типовых задач на взаимное расположение плоскости и прямой в пространстве.

Задача 1. Дана плоскость 3x + 2y — z + 1 = 0 и прямая r: X = t; Y = -1; Z = 2t + 1. Требуется определить положение прямой относительно плоскости и найти угол между ними.

Решение. Составляем уравнения прямой в каноническом виде: r: x(t) = t, y(t) = -1, z(t) = 2t + 1. Подставляем любую точку прямой, например X = 0, Y = -1, Z = 1, в уравнение плоскости: 3*0 + 2*(-1) — 1 + 1 = 0. Значит, прямая пересекает плоскость. Находим вектор нормали плоскости: N = (3; 2; -1). Вектор направления прямой: V = (1; 0; 2). Скалярное произведение: (N,V) = 3. По формуле: cos θ = |(N,V)|/|N|*|V| = 3/√14. Угол между прямой и плоскостью составляет примерно 9 градусов.

Задача 2. Определить положение прямой, заданной уравнениями X = Y = Z, относительно плоскости x+y+z = 1 и найти расстояние от начала координат до плоскости вдоль прямой.

Решение. Плоскость проходит через точку (1; 0; 0), нормальный вектор (1; 1; 1). Принадлежащая прямой точка X = Y = Z = 1 удовлетворяет уравнению плоскости. Значит, прямая лежит в плоскости. Расстояние по прямой от начала координат до плоскости равно длине отрезка от (0; 0; 0) до (1; 1; 1), то есть √3.

Задача 3. Через прямую L: x = 1 + 2t; y = 3 − t; z = 2t и точку A(5; −1; 4) провести плоскость α. Найти угол между плоскостью 2x − y + z = 1 и плоскостью α.

Решение. Записываем уравнение плоскости α в виде α: (x − 5) + λ(1 + 2t) + μ(2 − t) = 0. Подставляем координаты точки A и получаем: λ + μ = 0. Выбираем, например, λ = 1, μ = −1. Тогда уравнение плоскости α: (x − 5) + (1 + 2t) − (2 − t) = 0 или x + z = 9. Находим нормальный вектор плоскости 2x − y + z = 1: N1 = (2; −1; 1). Для плоскости α: N2 = (1; 0; 1). Скалярное произведение векторов равно 2. Косинус угла между плоскостями θ = 2/√6, а сам угол θ = arccos(2/√6) ≈ 49°.

В данных примерах решаются наиболее распространенные задачи на нахождение взаимного расположения прямой и плоскости, угла между объектами, заданными в пространстве.

Рекомендации по составлению уравнений

При решении задач на взаимное расположение плоскости и прямой в пространстве важно правильно записать их уравнения. Рассмотрим основные рекомендации.

1. Для задания плоскости удобнее всего использовать общее уравнение первой степени: Ax + By + Cz + D = 0. Коэффициенты A, B, C находятся как компоненты вектора нормали к плоскости.
2. Прямая в пространстве задается или каноническими уравнениями через точку и направляющий вектор, или параметрическими уравнениями.
3. Чтобы найти точку пересечения прямой и плоскости, нужно приравнять правые части параметрических уравнений прямой к нулю и решить полученную систему относительно параметра.

Также важно верно определить взаимное расположение прямой и плоскости в пространстве. Существует 3 основных случая:

1. Прямая пересекает плоскость в некоторой точке.
2. Прямая параллельна плоскости.
3. Прямая лежит в плоскости.

Чтобы определить, какой случай имеет место, нужно подставить координаты некоторой точки прямой в уравнение плоскости и проанализировать результат:

• Если равенство выполняется, значит, прямая лежит в плоскости или пересекает ее.
• Если подстановка дает неравенство, а скалярное произведение векторов нормали плоскости и направления прямой отлично от нуля, то прямая пересекает плоскость.
• Если подстановка дает неравенство, а скалярное произведение равно нулю, значит прямая параллельна плоскости.

Полезные советы для решения задач

Рассмотрим несколько полезных советов, которые помогут решать задачи на взаимное расположение плоскости и прямой в пространстве.

1. Внимательно прочитайте условие задачи, выпишите отдельно дано и требуется. Это поможет структурировать информацию и не упустить важные детали.
2. Запишите уравнения плоскости и прямой в удобном для вас виде, проверив, что они заданы корректно. Лучше использовать общее уравнение плоскости и параметрические уравнения прямой.
3. Графически изобразите взаимное расположение объектов, если это возможно. Чертеж всегда облегчает понимание условия.

После этого можно приступать непосредственно к решению задачи в такой последовательности:

1. Определите взаимное расположение прямой и плоскости, подставив координаты некоторой точки прямой в уравнение плоскости.
2. Если прямая пересекает плоскость, найдите точку их пересечения.
3. Если нужно, вычислите угол между прямой и плоскостью по формуле через скалярное произведение.
4. Ответьте на все вопросы, поставленные в задаче.

Кроме того, полезно знать некоторые частные случаи задач:

• Чтобы найти ортогональную проекцию прямой на плоскость, нужно решить систему из уравнений этой плоскости и прямой.
• Для нахождения расстояния от точки до прямой используется известная формула через скалярное и векторное произведения.
• Чтобы провести плоскость, перпендикулярную данной прямой и проходящую через точку, берется вектор направления прямой за нормальный вектор плоскости.